Modal Analysis of a 4 Story Shear Building

[ Problem Description ] [ Input File ] [ Output File ] [ Analysis Results ]

In this example we compute the eigenvalues, natural periods of vibaration, and modal shapes for a 4 story shear building.

PROBLEM DESCRIPTION

Figure 1 is a schematic of the 4 story shear building, and its corresponding mass and stiffness matrices.

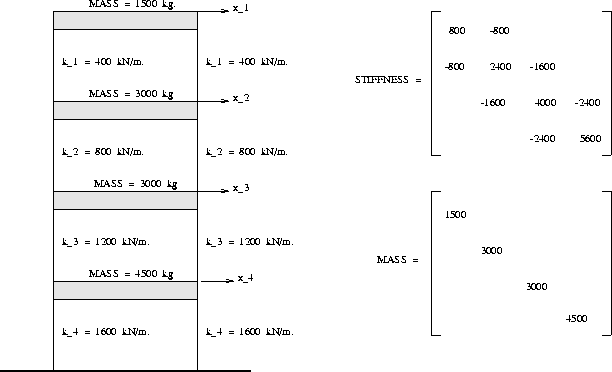
A simplified model of the building is obtained by assuming that all of the building mass is lumped at the floor levels, that the floor beams are rigid, and that the columns are axially rigid. Together these assumptions allow for the generation of a model commonly known as a shear-type building model, where displacements at each floor level may be described by one degree-of-freedom alone. Hence, only four degrees of freedom are needed to describe total displacements of the structure.

INPUT FILE

We employ a three-part input file to define the mass and stiffness matrices, solve the eigenproblem, and print the corresponding eigenvectors and natural periods of vibrations. Details of the ALADDIN input file are as follows:

   /* [a] : Define working variables for eigenproblem analysis */

   no_eigen = 4;

   /* [b] : Form mass and stiffness matrices */

   mass = ColumnUnits( 1500*[ 1, 0, 0, 0;
                              0, 2, 0, 0;
                              0, 0, 2, 0;
                              0, 0, 0, 3], [kg] );

   stiff = ColumnUnits( 800*[ 1, -1,  0,  0;
                             -1,  3, -2,  0;
                              0, -2,  5, -3;
                              0,  0, -3,  7], [kN/m] );

   PrintMatrix(mass, stiff);

   /* [c] : Compute and print eigenvalues, natural periods of */
   /*       vibration, and eigenvectors.                      */

   eigen       = Eigen(stiff, mass, [no_eigen]);
   eigenvalue  = Eigenvalue(eigen);
   eigenvector = Eigenvector(eigen);

   for(i = 1; i <= no_eigen; i = i + 1) {
       print "Mode", i ," : w^2 = ", eigenvalue[i][1];
       print " : T = ", 2*PI/sqrt(eigenvalue[i][1]) ,"\n";
   }

   PrintMatrix(eigenvector);

Points to note:

• The parameter no_eigen stores the number of eigenvalues and eigenvectors to be computed by the Subsspace iteration algorithm.
• The matrix eigenvalue has 4 columns and 1 row, and stores the circular natural frequency squared, for each of the periods of vibration.
• The modal shapes are stored in the columns of matrix eigenvector .

OUTPUT FILE

We have used the parameter no_eigen to control the number of eigenvalues/vectors that are computed by the subspace iteration, and printed.

    MATRIX : "mass"

    row/col                  1            2            3            4   
            units           kg           kg           kg           kg   
       1            1.50000e+03  0.00000e+00  0.00000e+00  0.00000e+00
       2            0.00000e+00  3.00000e+03  0.00000e+00  0.00000e+00
       3            0.00000e+00  0.00000e+00  3.00000e+03  0.00000e+00
       4            0.00000e+00  0.00000e+00  0.00000e+00  4.50000e+03

    MATRIX : "stiff"

    row/col                  1            2            3            4   
            units          N/m          N/m          N/m          N/m   
       1            8.00000e+05 -8.00000e+05  0.00000e+00  0.00000e+00
       2           -8.00000e+05  2.40000e+06 -1.60000e+06  0.00000e+00
       3            0.00000e+00 -1.60000e+06  4.00000e+06 -2.40000e+06
       4            0.00000e+00  0.00000e+00 -2.40000e+06  5.60000e+06

    *** SUBSPACE ITERATION CONVERGED IN  2 ITERATIONS 

    Mode         1  : w^2 =      117.8 1/sec^2  : T =     0.5789 sec 
    Mode         2  : w^2 =      586.5 1/sec^2  : T =     0.2595 sec 
    Mode         3  : w^2 =       1125 1/sec^2  : T =     0.1873 sec 
    Mode         4  : w^2 =       2082 1/sec^2  : T =     0.1377 sec 

    MATRIX : "eigenvector"

    row/col                  1            2            3            4   
            units                                                       
       1            1.00000e+00  1.00000e+00 -9.01452e-01  1.54356e-01
       2            7.79103e-01 -9.96248e-02  1.00000e+00 -4.48172e-01
       3            4.96553e-01 -5.39887e-01 -1.58595e-01  1.00000e+00
       4            2.35062e-01 -4.37613e-01 -7.07973e-01 -6.36879e-01

ANALYSIS RESULTS

Figure 2 shows the four modal shapes of vibration and associated natural periods of vibration.

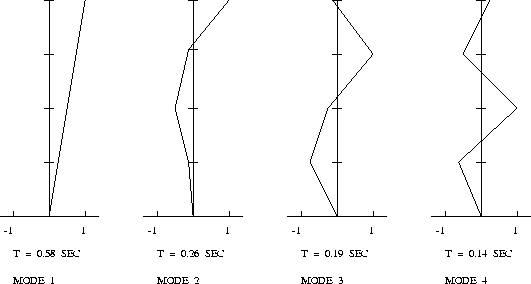
Points to note:

• The left-most column of matrix eigenvector stores the first mode of vibration, the second left-most column the second mode of vibration, and so forth.
• In interpreting the physical meaning of each mode, you should notice that the structural degrees of freedom x_1 ... x_4 progress from the roof down to the first floor. Hence for mode 1, the largest modal displacement is at the roof-level (as expected).
• The number of sign changes in the modal shapes increases with the modal number. From the matrix eigenvector, and Figure 2, we see that there are no sign changes in mode 1, one sign change in mode 2, two sign changes in mode 3, and three sign changes in mode 4.