|
SPIKE SOLUTIONS FOR THE CUBIC NONLINEARITY
ACTIVATOR-INHIBITOR SYSTEM
|
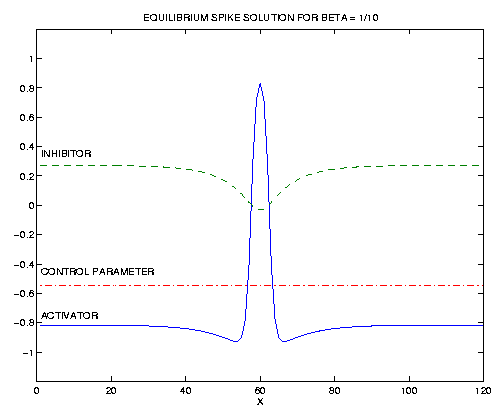
This
MPEG movie shows how the equilibrium spike
solution can be obtained by temporarily raising the control parameter
above threshold in the location where the spike is desired.
Only the activator is pictured, but the inhibitor and control, like the
activator, are approximately rotations of the corresponding one-dimensional
functions.
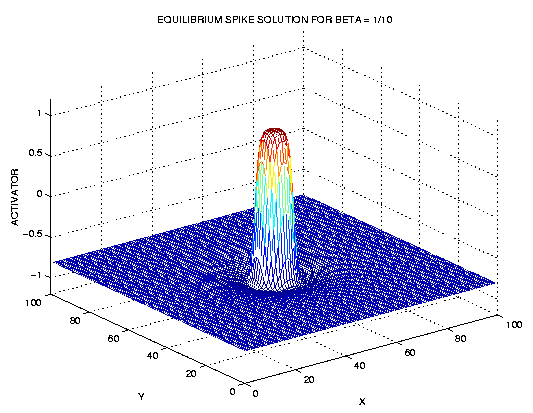
This
MPEG movie shows how the equilibrium spike
solution can be obtained by temporarily raising the control parameter
above threshold in the location where the spike is desired for the
two-dimensional system.
|
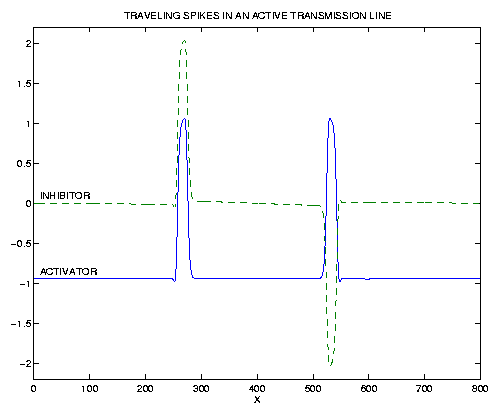
TRAVELING SPIKES IN AN ACTIVE TRANSMISSION LINE
|
For the active transmission line, solutions decay to a stable
traveling spike solution for any initial excitation in the region of
attraction of the traveling spike solution.
The traveling spikes are excited by initial conditions rather than by locally
raising the control parameter. This
MPEG movie shows
the traveling spikes forming, traveling, and interacting with each other.
In a linear transmission line, the oppositely-traveling waves would not
change shape as a result of passing through each other. However, for
the active transmission line, the interactions temporarily change the
spike shapes due to the nonlinearity. However, after traveling a certain
distance, the spike shapes decay to the stable traveling spike solution
again.
|
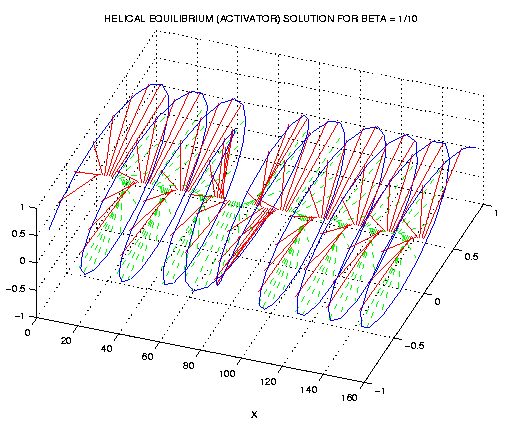
HELICAL SOLUTION FOR THE COMPLEX ACTIVATOR-INHIBITOR
EQUATION
|
The complex activator-inhibitor equation with C=0 has a
stable helical equilibrium solution. Since random initial conditions
were used, there are fronts between the left-handed and right-handed
ideal helixes in the above figure. In the coupled oscillator context,
this figure represents the equilibrium phases of the oscillators.
This
MPEG movie shows the helical equilibrium
being reached from random initial conditions.
This
MPEG movie shows the evolution of the
states of the oscillators, in the coupled oscillator context. The
state evolution is simply the phase evolution rotated at the common
frequency of the oscillators. Note that right-handed and left-handed
helical waves ``travel'' in opposite directions.
Page maintained by Eric Justh. Send comments to
justh@eng.umd.edu
Last Updated: August 18, 1998.