 Vibration of Supported Cantilever Beam
Vibration of Supported Cantilever Beam
 Vibration of Supported Cantilever Beam
Vibration of Supported Cantilever Beam
[ Problem Description ]
[ Supported Cantilever Beam ]
[ Input File ]
[ Output File ]
The purpose of this numerical example is to demonstrate the use of:
We have deliberately selected a problem with a small number of unknowns so that step-by-step details of items [1] and [2] may be written down, and solved using functions from the matrix library alone.
Figure 1 shows uniform cantilever beam with a supported end point.
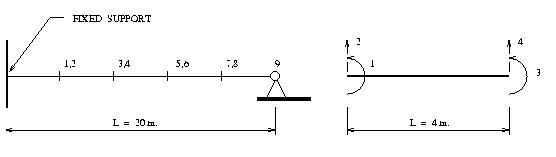
The cantilever has a length of 20 m, modulus of elasticity E=200 GPa, and a constant moment of inertia along its length of I = 15.5 mm^4. We will assume that the cantilever is rigid in its axial direction, and that all deformations are small. The boundary conditions are full-fixity at the base and zero translational displacement at the cantilever end.
Overall behavior of the cantilever will be modeled with five beam finite elements, and nine global degrees of freedom.They are a translation and rotation at each of the internal nodes, and a single rotational degree of freedom at the hinged cantilever support. Numbering for the global degrees of freedom is shown on the left-hand side of figure 1. Lateral displacements along each beam element will be expressed as the superposition of four cubic interpolation functions, each weighted by a nodal displacement factor. The four nodal displacements are two beam-end lateral displacements, and two beam-end rotations, as shown on the right-hand side of the Figure 1.
A finite element model for the supported cantilever is defined in parts [a] to [f] of the following input file. The eigenvalue problem is solved in part [g].
/* [a] : Define section/material properties */
E = 200000 MPa;
I = 15.5E+6 mm^4;
L = 4 m;
mbar = 31.6 kg/m;
/* [b] : Define (4x4) stiffness matrix for beam element */
stiff = Matrix([4,4]);
stiff = ColumnUnits( stiff, [N, N/m, N, N/m] );
stiff = RowUnits( stiff, [m], [1] );
stiff = RowUnits( stiff, [m], [3] );
stiff[1][1] = 4*E*I/L;
stiff[1][2] = 6*E*I/(L^2);
stiff[1][3] = 2*E*I/L;
stiff[1][4] = -6*E*I/(L^2);
stiff[2][1] = 6*E*I/(L^2);
stiff[2][2] = 12*E*I/(L^3);
stiff[2][3] = 6*E*I/(L^2);
stiff[2][4] = -12*E*I/(L^3);
stiff[3][1] = 2*E*I/L;
stiff[3][2] = 6*E*I/(L^2);
stiff[3][3] = 4*E*I/L;
stiff[3][4] = -6*E*I/(L^2);
stiff[4][1] = -6*E*I/(L^2);
stiff[4][2] = -12*E*I/(L^3);
stiff[4][3] = -6*E*I/(L^2);
stiff[4][4] = 12*E*I/(L^3);
PrintMatrix(stiff);
/* [c] : Define (4x4) consistent mass matrix for beam element */
mass = Matrix([4,4]);
mass = ColumnUnits( mass, [ kg*m, kg, kg*m, kg] );
mass = RowUnits( mass, [m], [1] );
mass = RowUnits( mass, [m], [3] );
mass[1][1] = (mbar*L/420)*4*L*L;
mass[2][1] = (mbar*L/420)*22*L;
mass[3][1] = (mbar*L/420)*-3*L^2;
mass[4][1] = (mbar*L/420)*13*L;
mass[1][2] = (mbar*L/420)*22*L;
mass[2][2] = (mbar*L/420)*156;
mass[3][2] = (mbar*L/420)*-13*L;
mass[4][2] = (mbar*L/420)*54;
mass[1][3] = (mbar*L/420)*-3*L^2;
mass[2][3] = (mbar*L/420)*-13*L;
mass[3][3] = (mbar*L/420)*4*L^2;
mass[4][3] = (mbar*L/420)*-22*L ;
mass[1][4] = (mbar*L/420)*13*L;
mass[2][4] = (mbar*L/420)*54;
mass[3][4] = (mbar*L/420)*-22*L; mass[4][4] = (mbar*L/420)*156;
PrintMatrix(mass);
/* [d] : Destination Array beam element connectivity */
LD = [ 0, 0, 1, 2 ;
1, 2, 3, 4 ;
3, 4, 5, 6 ;
5, 6, 7, 8 ;
7, 8, 9, 0 ];
/* [e] : Allocate memory for global mass and stiffness matrices */
GMASS = Matrix([9,9]);
GMASS = ColumnUnits( GMASS, [ kg*m, kg, kg*m, kg, kg*m, kg, kg*m, kg, kg*m ] );
GMASS = RowUnits( GMASS, [m], [1] );
GMASS = RowUnits( GMASS, [m], [3] );
GMASS = RowUnits( GMASS, [m], [5] );
GMASS = RowUnits( GMASS, [m], [7] );
GMASS = RowUnits( GMASS, [m], [9] );
GSTIFF = Matrix([9,9]); GSTIFF = ColumnUnits( GSTIFF, [ N, N/m, N, N/m, N, N/m, N, N/m, N ] );
GSTIFF = RowUnits( GSTIFF, [m], [1] );
GSTIFF = RowUnits( GSTIFF, [m], [3] );
GSTIFF = RowUnits( GSTIFF, [m], [5] );
GSTIFF = RowUnits( GSTIFF, [m], [7] );
GSTIFF = RowUnits( GSTIFF, [m], [9] );
/* [f] : Assemble Global Stiffness/Mass Matrices for Two Element Cantilever */
no_elements = 5;
for( i = 1; i <= no_elements; i = i + 1) {
for( j = 1; j <= 4; j = j + 1) {
row = LD [i][j];
if( row > 0) {
for( k = 1; k <= 4; k = k + 1) {
col = LD [i][k];
if( col > 0) {
GMASS [ row ][ col ] = GMASS [ row ][ col ] + mass[j][k];
GSTIFF[ row ][ col ] = GSTIFF[ row ][ col ] + stiff[j][k];
}
}
}
} }
/* [g] : Compute and Print Eigenvalues and Eigenvectors */
no_eigen = 2;
eigen = Eigen( GSTIFF, GMASS, [ no_eigen ]);
eigenvalue = Eigenvalue(eigen);
eigenvector = Eigenvector(eigen);
for(i = 1; i <= no_eigen; i = i + 1) {
print "Mode", i ," : w^2 = ", eigenvalue[i][1];
print " : T = ", 2*PI/sqrt(eigenvalue[i][1]) ,"\n";
}
PrintMatrix(eigenvector);
Points to note are:
Details of the beam element stiffness and mass matrices, and ensuing eigenvalues and eigenvectors are as follows:
MATRIX : "stiff"
row/col 1 2 3 4
units N N/m N N/m
1 m 3.10000e+06 1.16250e+06 1.55000e+06 -1.16250e+06
2 1.16250e+06 5.81250e+05 1.16250e+06 -5.81250e+05
3 m 1.55000e+06 1.16250e+06 3.10000e+06 -1.16250e+06
4 -1.16250e+06 -5.81250e+05 -1.16250e+06 5.81250e+05
MATRIX : "mass"
row/col 1 2 3 4
units kg.m kg kg.m kg
1 m 1.92610e+01 2.64838e+01 -1.44457e+01 1.56495e+01
2 2.64838e+01 4.69486e+01 -1.56495e+01 1.62514e+01
3 m -1.44457e+01 -1.56495e+01 1.92610e+01 -2.64838e+01
4 1.56495e+01 1.62514e+01 -2.64838e+01 4.69486e+01
*** SUBSPACE ITERATION CONVERGED IN 7 ITERATIONS
Mode 1.0000e+00 : w^2 = 145.8 rad.sec^-2.0 : T = 0.5203 sec
Mode 2.0000e+00 : w^2 = 1539 rad.sec^-2.0 : T = 0.1602 sec
MATRIX : "eigenvector"
row/col 1 2
units
1 1.24900e-01 -2.28500e-01
2 m 3.02715e-01 -7.71256e-01
3 1.03061e-01 1.77895e-01
4 m 8.01556e-01 -9.46803e-01
5 -1.29310e-02 3.44764e-01
6 m 1.00000e+00 3.03399e-01
7 -1.37281e-01 -5.51890e-02
8 m 6.87189e-01 1.00000e+00
9 -1.89640e-01 -3.58198e-01
Points to note are:
Figure 2 shows the mode shapes and natural periods of vibration for the supported cantilever beam.

We have drawn the mode shapes as connected straight lines -- actually, the mode shapes will be cubic splines, as defined by the beam element shape functions.