 Plane Strain Analysis of Pipe Cross Section
Plane Strain Analysis of Pipe Cross Section
 Plane Strain Analysis of Pipe Cross Section
Plane Strain Analysis of Pipe Cross Section
[ Problem Statement ]
[ Finite Element Mesh ]
[ Displacements ]
[ Stress Contours ]
[ Input/Output Files ]
You will need Aladdin 2.0 to run this problem.
Figure 1 shows an elevation and cross sectional view of a pipe

loaded by two-line loads P = 12 kN/m. The inside and outside diameters of the pipe are 20 cm and 30 cm, respectively. We assume that the pipe is fully-fixed in its longitudinal direction (i.e., strains in the longitudinal direction are zero). The material properties are Young's modulus = 200 GPa and Poisson's ration = 1/3.
This example presents a finite element analysis of the steel pipe cross-section, assuming plane-strain behavior. We will:
Because the pipe cross section has axes of symmetry on both the horizontal and vertical axes, we need only model 1/4 of the pipe cross section.

Figure 2 is a MATLAB plot of the 1/4 pipe cross section. Although the finite elements will be represented by a (x,y) cartesian coordinate system, the mesh is most easily generated with a (radius, angle) polar coordinate system. The block of code:
radius_min = 10.0 cm; angle_min = 0.0;
radius_max = 15.0 cm; angle_max = PI/2;
radius_incr = 0.5 cm; angle_incr = PI/16;
node = 0;
angle = angle_min;
while( angle <= angle_max ) {
radius = radius_min;
while( radius <= radius_max ) {
node = node + 1;
x = radius*cos(angle);
y = radius*sin(angle);
if ( abs(x) <= 0.0000001 cm ) { x = 0.0 cm; }
if ( abs(y) <= 0.0000001 cm ) { y = 0.0 cm; }
AddNode(node, [ x, y]);
radius = radius + radius_incr;
}
angle = angle + angle_incr;
}
generates the circular grid of 99 nodes
=================================================
Node x (cm) y (cm)
=================================================
1 10.0 0.0
2 10.5 0.0
3 11.0 0.0
...........
98 0.0 14.5
99 0.0 15.0
=================================================
We use the test:
if ( abs(x) <= 0.0000001 cm ) { x = 0.0 cm; }
if ( abs(y) <= 0.0000001 cm ) { y = 0.0 cm; }
to ensure that nodes along the horizontal and vertical axes are "exactly" positioned.
Eighty finite elements are attached to the nodes with the block of commands:
nodeno = 0; elmtno = 0;
for ( i = 0; i < 8; i = i + 1 ) {
nodeno = 11*i;
for ( j = 1; j <= 10; j = j + 1 ) {
nodeno = nodeno + 1;
elmtno = elmtno + 1;
AddElmt( elmtno, [ nodeno, nodeno + 1, nodeno + 12, nodeno + 11 ], "pipe" );
}
}
Section and Material Properties
The block of code:
ElementAttr("pipe") { type = "PLANE_STRAIN";
section = "mysection";
material = "mymaterial"; }
SectionAttr("pipesection") { depth = 30 cm;
width = 30 cm; }
MaterialAttr("pipematerial") { poisson = 1/3;
yield = 36000;
E = 200 GPa; }
defines the material properties and plain-strain modeling assumption for the "pipe" element attribute.
Boundary Conditions
We assume that nodes along the vertical axis (i.e., x = 0) are restrained in the x-direction but can freely move in the y-direction. The block of commands:
for (ii = 1; ii <= 11; ii = ii + 1 ) {
FixNode( ii , [0,1] );
}
applies this boundary condition to nodes 1 through 11.
Similarly, nodes along the horizontal axis (i.e., y = 0) are fixed in the vertical direction, but allowed to freely displace in the horizontal direction.
After the boundary conditions have been applied, the finite element model has 176 degrees of freedom.
External Loads
We assume that each half of the pipe section carries 6 kN/cm, exactly, ahd that the loads are carried by equally by nodes in the two uppermost finite elements. The block of commands:
Fx = 0.0 kN; Fy = 3.0 kN;
NodeLoad( 88, [ Fx, -Fy ]);
NodeLoad( 99, [ Fx, -Fy ]);
applies nodal loads of -3.0 kN to nodes 88 and 89.
Only three Aladdin statements:
stiff = Stiff();
eload = ExternalLoad();
displ = Solve(stiff, eload);
are needed to for the stiffness matrix, external load vector, and compute the displacements. The command:
PrintDispl(displ);
generates the output:
==========================================
Node Displacement
No displ-x displ-y
==========================================
units m m
1 -2.60880e-08 0.00000e+00
2 -2.63854e-08 0.00000e+00
3 -2.65135e-08 0.00000e+00
4 -2.63598e-08 0.00000e+00
........
97 0.00000e+00 -4.45024e-08
98 0.00000e+00 -5.45846e-08
99 0.00000e+00 -9.30605e-08
==========================================
As expected, the nodes along the vertical axis move downwards under the vertically applied loads. Intuition also dictates that the nodes along the horizontal axis will move outwards -- the numerical results indicate, however, a small displacement inwards.
Plotting the Stress Contours
Figures 3 and 4 show the distribution of finite element stresses in the horizontal and vertical directions, respectively.
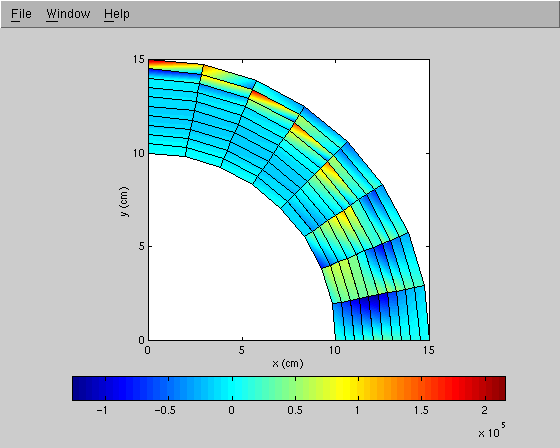

Rather that produce a smooth countour map of element stress components over the pipe cross section, we have deliberately chosen to plot the stresses within each finite element, and to highlight discontinuities across element boundaries.
While it is probably not a good idea to rely on the accuracy of stresses within any particular element, collectively the distributions of stresses can be used to validate our calculations. You should notice in Figure 3, for example, that the average color of the elements along the vertical axis is almost the same as those elements along the horizontal axiis. Since the pipe wall thickness is the same in both cases, we can deduce that in an overall sense, forces in the horizontal direction sum to zero.
Similarly, the stress contours in Figure 4 can be used to validate equilibrium of forces in the vertical direction. From the color code bar we see that "dark blue" corresponds to a vertical stress of about -1.2 x 10000 Pa. Given that the thickness of the pipe wall is 5 cm, it follows that the external loads should be approximately:
External load = 1.2 x 10000 Pa * 5 cm
= 6.0 kN / m.
Hence the vertical stresses along the horizontal axis are balanced by the externally applied loads a nodes 88 and 99.
Extrapolation of Stresses to Nodal Coordinates
By default the isoparametric plane-strain/plane-stress element will compute and print stress components at the gaussian points of integration. This is where evaluation of the stresses is most accurate.
The block of code:
M = Zero([4,4]); M[1][1] = (sqrt(3) + 1)^2; M[1][2] = 2; M[1][3] = (sqrt(3) - 1)^2; M[1][4] = 2; M[2][1] = 2; M[2][2] = (sqrt(3) + 1)^2; M[2][3] = 2; M[2][4] = (sqrt(3) - 1)^2; M[3][1] = (sqrt(3) - 1)^2; M[3][2] = 2; M[3][3] = (sqrt(3) + 1)^2; M[3][4] = 2; M[4][1] = 2; M[4][2] = (sqrt(3) - 1)^2; M[4][3] = 2; M[4][4] = (sqrt(3) + 1)^2; T = Inverse((1/12)*M);
sets up a (4x4) transformation matrix T that will extrapolate stresses at the 4 internal gauss points out to the nodal coordinates. With the matrix T in place, we can now systematically use
actions = GetStress( [ii], displ );
to retrieve the stresses for element "ii" and then compute
and print the "approximate" stresses at the nodal coordinates.
The complete block of code is:
print "\n";
print "Element Stresses (sigma_xx at the nodal points)\n";
print "===============================================\n\n";
for( ii = 1; ii <= 80; ii = ii + 1 ) {
/* retrieve stresses and extrapolate out to nodal coordinates */
actions = GetStress( [ii], displ );
extrap = T*[ actions[1][3];
actions[2][3];
actions[3][3];
actions[4][3] ];
/* map extrapolated stresses onto nodal coordinate system */
extrap = [ 0, 0, 1, 0;
0, 0, 0, 1;
1, 0, 0, 0;
0, 1, 0, 0 ] * extrap;
/* print extrapolated stresses in format for MATLAB plotting */
print ii;
print QDimenLess(extrap[1][1]);
print QDimenLess(extrap[2][1]);
print QDimenLess(extrap[3][1]);
print QDimenLess(extrap[4][1]);
print "\n";
}
Points to note:
[ 0, 0, 1, 0;
0, 0, 0, 1;
1, 0, 0, 0;
0, 1, 0, 0 ]
simply reorders the extrapolated stresses so that they match the nodal points.