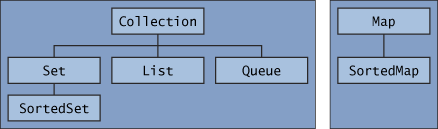
Figure 01. Hierarchy of interfaces in the Java Collections Framework.
Now that we know how to create objects, the next subject of importance is how to organize large collections of objects so that they are easy to store, easy to find, and easy to modify.
A collection
is an object that groups multiple elements into a single unit.
Typically, they represent data items that form a natural group:
Collections are used to store, retrieve, manipulate, and communicate aggregate data.
Collections Framework
A collections framework is a unified architecture for representing and manipulating collections. Collections frameworks:
The Java Collections framework is a set of utility classes and interfaces (located in the java.util package) for working with collections of objects.
Collections frameworks contain the following:
These are abstract data types that represent collections. Interfaces allow collections to be manipulated independently of the details of their representation.
These are the concrete implementations of the collection interfaces. In essence, they are reusable data structures.
These are the methods that perform useful computations, such as searching and sorting, on objects that implement collection interfaces.
The Java Collections interfaces are organized as follows:

Figure 01. Hierarchy of interfaces in the Java Collections Framework.
The collections functionality includes:
Collections are used to store, retrieve, manipulate, and communicate aggregate data (groups of objects). Typically, they represent data items that form a natural group.
General Purpose Implementations
A simplified view of the relationship between containers and the Set, List and Map interfaces is as follows:
| Interfaces | Hash Table |
Resizeable Array |
Balanced Tree |
Linked List |
| Set | HashSet | TreeSet | ||
| List | ArrayList | LinkedList | ||
| Map | HashMap | TreeMap |
In practice, an implementation will follow:
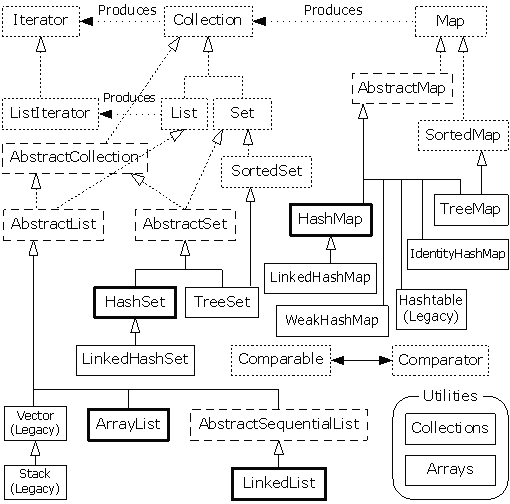
Figure 02. Taxonomy of interfaces, abstract classes, and concrete classes in the Java Collections Framework.
Points to note:
The solid arrows show that a class can produce objects of the class the arrow is pointing to. For example, any Collection can produce an Iterator and a List can produce a ListIterator (as well as an ordinary Iterator, since List is inherited from Collection).
| PART 1. WORKING WITH ARRAY LISTS | |
|
Program 01. Array List1
This program demostrates the use of the arraylist construct to create
lists of "strings" and lists of edges and nodes in a polygon.
|
Code: ArrayTest1.java Edge.java , Node.java , Vector.java Program output |
|
Program 02. Array List2
This program uses the arraylist construct to create a list of triangle objects.
Each triangle contains references to three edge and three nodal point objects.
|
Code: ArrayTest2.java Triangle.java , Edge.java , Node.java , Vector.java Program output |
|
Program 03. Array List
This program demonstrates more of the advanced features of array lists,
including the ability to store more than one object type,
retrieve the position of an object having a certain name,
retrieve neighboring -- next and previous -- objects.
|
Code:
ArrayListExample.java Program output |
 Program 03. Arraylist Model of the Simpsons
Program 03. Arraylist Model of the Simpsons
This program creates Person objects for Homer Simpson, Bart Simpson, Lisa Simpson and Abe Simpson (Bart and Lisa's grandfather), and then connects these objects together within the framework of a family. In simple terms, Figure 03 says:
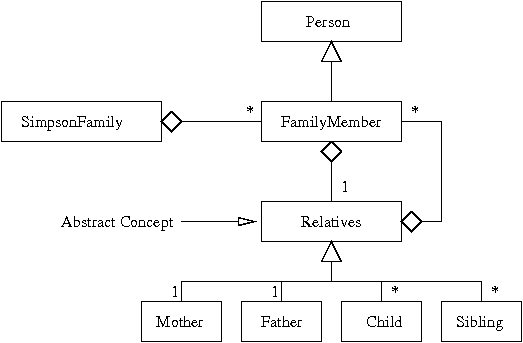
Figure 04.
UML class diagram for relationships among Person, FamilyMember, Relatives is a generalized (or abstract) concept for the set of family members that fullfil the roles of father, mother, spouse, children and siblings. Each person object is instantiated with the relevant name and date of birth. Then the objects are added to an array list and printed by walking along the list. Notice how the toString() method in Person is used to print the abbreviated details of a person's credentials.
Finally, the person objects are ordered according to their age --
from youngest to oldest. Because an arraylist is a Collection,
we can use the sort() method in Collections to take care of the details.
All that we have to provide is a method to compare relative age
of two person objects. These details can be found in Family.java.
|
Code:
Person.java
Family.java
Program output |
| PART 2. WORKING WITH SETS | |
|
Program 05. Create HashSet of Strings
Demonstrate usse of a HashSet to print all unique words read from System.in. The test input file is as follows:
Here is the shortest sentence in the english language that contains all twenty six letters. The quick brown fox jumps over the lazy dog. And now for a few more words just to increase the number of distinct words. dog. dog. dog. dog. dog. |
Code: TestHashSet.java
Program output |
|
Program 06. Create HashSet of Enumerated Data Types
Demonstrate use of a hashset of enumerated data types -- days of the week.
|
Code:
TestHashSetEnumeration.java
Program output |
| PART 3. WORKING WITH HASH TABLES AND MAPS | |
|
Program 07. Simple HashMap of Employees
This program demonstrates the use of a map with
key type String and value type Employee.
|
Code: TestHashMap.java Employee.java Program output |
|
Program 08. Count Frequency of Words in a Document
This program reads a stream of words from the keyboard. The test input file is: This is the test file. Here is the shortest sentence in the English language that contains all twenty six letters. The quick brown fox jumps over the lazy dog.
First, this program uses a hashmap to record the frequency of each word.
It then uses a treemap to order the words.
|
Code: CountWordFrequency.java Program output |
|
Program 09. Simple Implementation for a Symbol Table
A symbol table is a data type that associates a value with a key. Users store (put) an entry by specifying the key-value pair. They they can retrieve (get) a value corresponding to a particular key. While the key is always assumed to be a String, the value can be any Object. When two inputs hash to the same key, then items are chained into a linked list, e.g.,
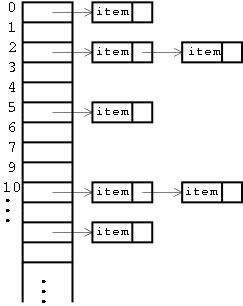
Figure 05. Layout of memory in a hash table. Here is a very simple example. The fragment of code:
SymbolTable st = new SymbolTable();
st.put( "mark", "acura" );
st.put( "dianne", "bmw" );
stores two entries in the symbol table, namely, that "mark drives an acura" and "dianne drives a bmw." To retrieve these records from the symbol table, we write something like:
String s = "mark"
System.out.println ( s + " drives a " + st.get(s) );
String t = "dianne"
System.out.println ( t + " drives a " + st.get(t) );
The example code creates a series of MetroStation objects, which are then stored in the symbol table.
Then an array of "metro station names" are defined for
the red and green lines. The corresponding metro station
objects are retrieved from the symbol table, and
the "line" attribute is added to the metro station object description.
Some metro stations will service more than one metro line.
|
Code:
AdjList.java Edge.java MetroStation.java Node.java SymbolTable.java Track.java Vector.java Program output |
| PART 04. MODELING ASSOCIATION RELATIONSHIPS | |
|
Program 10. Uni-Directional Association
In a uni-directional association, two classes are related, but only one class knows that the relationship exists.

Figure 06. Uni-directional relationship between a customer and book.
In this example, we model the uni-directional association between
a customer and a book. The customer owns a book, but the book
is not aware of the customer.
|
Code: Book.java Customer.java TestRelationship.java
Program
output |
|
Program 11. Bi-Directional Association
By default, associations are assumed to be bi-directional. This means that both classes are aware of each other and their relationship. In this example we recode the customer-book association so that the customer owns a book and the book is owned by a customer, i.e.,
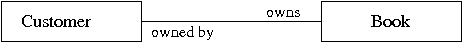
Figure 07. Bi-directional relationship between a customer and book.
The file TestRelationship.java assembles Customer and Book objects
and assembles the bi-directional association relationship.
Details of the association relationship are then printed from
the customer and book perspectives.
|
Code: Book.java Customer.java TestRelationship.java
Program
output |
|
Program 12. One-to-Many Associations
In a one-to-many relationship between classes A and B, each object of type A is linked to 0, 1 or many instances of object B. For example, if A and B represent company and employees, generally speaking, a specific company will have many employees. In this example we assemble a one-to-many association relationship between an academic department (CEE) and five students enrolled in the department.
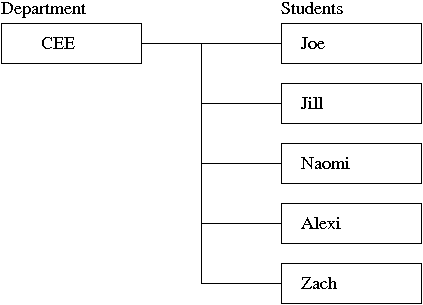
Figure 08. One-to-many association relationship between an academic department and students. |
Code: Department.java Main.java Student.java
Program
output |
|
Program 13. Many-to-Many Associations
A many-to-many relationship between classes A and B exists when multiple objects of type A associated with multiple objects of type B, and vise versa. For example, in most schools each teacher teaches multiple students and each student can be taught by multiple teachers. We now extend the one-to-many example, and assume that students may be enrolled in multiple departments.
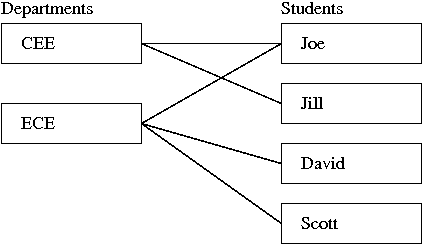
Figure 09. Many-to-many association relationships among academic departments and students.
SimSchool assembles the many-to-many relationship
between students and departments illustrated in Figure 09.
|
Code: Department.java SimSchool.java Student.java
Program
output |
| PART 05. CIVIL ENGINEERING APPLICATIONS | |
|
Program 14. Program Triangle and Point
There are lots of problems in Civil Engineering where we need to compute the relationship of a point (or set of points) to a shape. For example, in concrete design, we need to check that rebar has adequate cover. This problem can be abstracted as:
This program computes the distance of a point from the edge contour of a polygon.
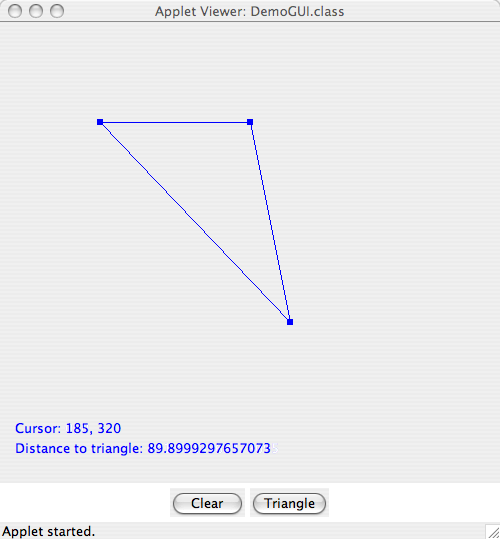
Figure 10. Screendump of triangle and point program
The triangle is composed of three edges and three nodes.
Each edge is simply a line segment.
Hence, the problem of computing the closest distance to the edge of the
triangle boils down to computing the distance of the point from each
edge and then taking the minumum value. These computations can be found
in Edge.java and Triangle.java, respectively.
|
Code: DemoGUI.java Edge.java Node.java Vector.java Triangle.java To compile the program, type: javac DemoGUI.java The program can be run as an applet. I just type: appletviewer DemoGUI.html where DemoGUI.html is a suitable file containing a reference to the point-and-triangle bytecode files. |
|
Program 15. Building Footprint
A footprint model simply defines the area that will be covered by an object. Footprint models of buildings are commonly used in the earliest stages of design and in high-level models of urban areas. Because the footprint area is defined by its perimeter, naturally, a general-purpose polygon model is the first approach that comes to mind. However, it turns out that the computation of simple polygon operations (e.g., computing the area) can quickly become very complicated. Many potentially difficult problems can be avoided by modeling the footprint as a collection of simple triangular regions. The next figure shows, for example, a six-triangle footprint model for the AV. Williams Building.

Figure 11. Footprint model for AV Williams Building Now let's move onto details of the software implementation.
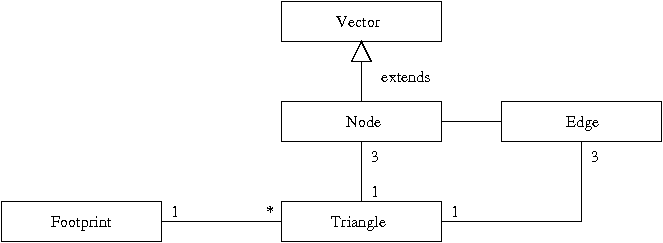
Figure 12. Class diagram for footprint implementation
Simply put, the adjacent figure says that one Footprint object will be composed of
many Triangle objects. In turn, triangles will be defined
in terms of Node and Edge objects. Nodes are an extension of Vector.
Properties of the building footprint (e.g., area, center of mass)
will be computed and summed across the ensemble of triangles.
|
Download the zipped source code . To compile the program, type: javac Footprint.java The program can be run as an application.
|
|
Program 16. Model of a Wheel Cross-Section
In this example we assemble a cross-section model of a wheel from triangle objects, and display the wheel cross section and its area in a graphics window. Pixel coordinates (as measured from the top left-hand corner of the graphics canvas) can also be printed on the canvas by moving the cursor to a desired position and then clicking.
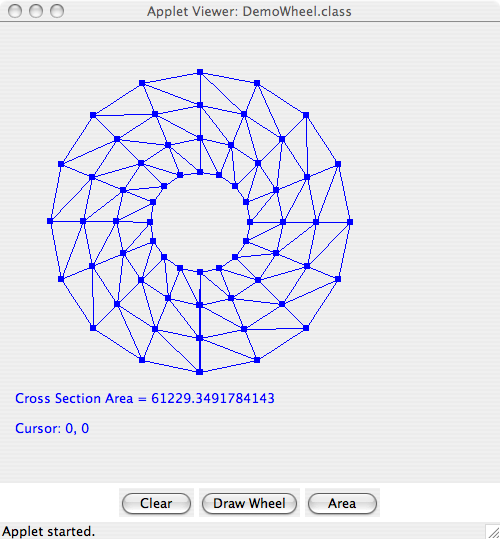
Figure 13. Cross section model of a Wheel. In this specific example, the minumum radius is 50 and the maximum radius is 150. Coordinates in the radial and angular directions are divided into three and sixteen intervals, repectively. Theoretical considerations indicate that the cross section will be 62,831. However, because the triangles only approximate the circular cross section, the computed area will be a little less. Individual triangle objects are assembled from Node and Edge objects, as shown above in the Footprint model. The wheel cross section is simply a collection of triangles stored in an array list.
The mesh of triangles in generated with a double loop. One loop increments
the coordinates from the minumum radius to the maximum radius.
A second loop systematically generates nodal coordiates in an angular
direction, from 0.0 through 2*pi radians.
|
Download the
zipped source code . To compile the program, type: javac DemoWheel.java The program can be run as an applet i.e., appletviewer DemoWheel.html |
|
Program 17. Centroid and Principal Axes of a Polygon Cross-Section
This program computes the engineering properties (cross section area; (x,y) coordinates of the centroid; moments of inertia about the centroid) for a polygon cross section, possibly containing holes.
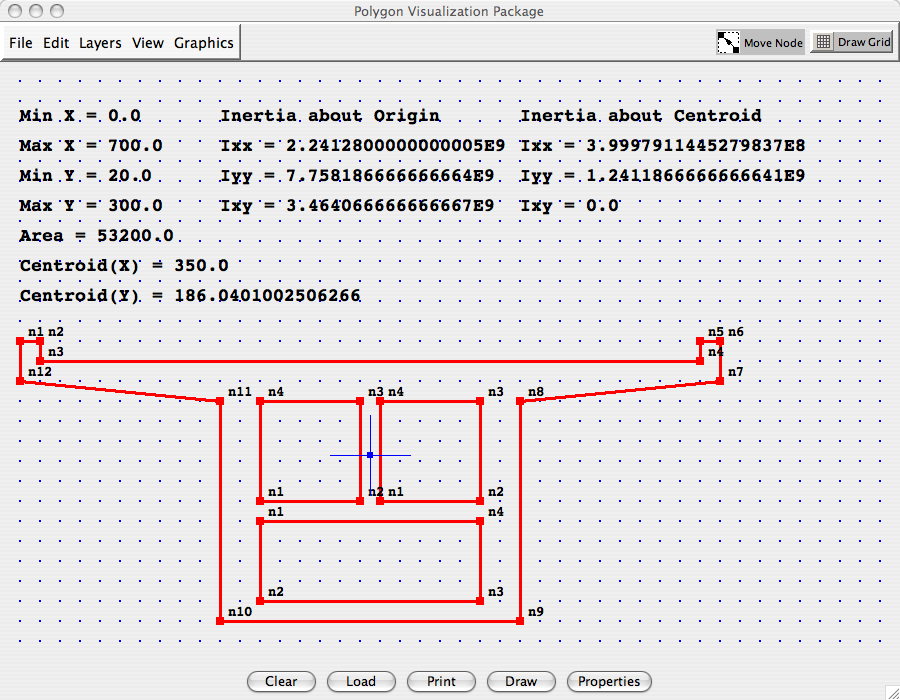
Figure 14. Screendump of bridge cross section and engineering properties ... Polygon cross sections are modeled as an exterior ring, possible containing multiple interior rings. Each ring corresponds to a list of nodes have (x,y) coordinates. The nodes in an exterior ring are stored in a clockwise direction. Interior rings (holes) have nodes stored in an anti-clockwise direction. Polygon cross sections are defined in an xml file. For example:
<?xml version="1.0" encoding="UTF-8"?>
<!-- Polygon Layout XML document -->
<!DOCTYPE polygon SYSTEM 'polygon.dtd'>
<polygon>
<loop type="exterior">
<coordinate> 100.0 0.0 </coordinate>
<coordinate> 100.0 200.0 </coordinate>
<coordinate> 300.0 200.0 </coordinate>
<coordinate> 300.0 0.0 </coordinate>
</loop>
</polygon>
defines a small square. |
Code: Rather than put individual java and xml files online, I have bundled them into a
tar file called BridgeAnalysis.tar .
To unpack the tar file, type:
tar xvf BridgeAnalysis.tar
The unpacked program will be in a directory called bridge-analysis.d. Move to that directory and then compile the program with the command:
javac PolygonGUI.java
To run the program, type:
appletviewer PolygonGUI.html
|
Last Modified in April 2012 by Mark Austin
Department of Civil and Environmental Engineering, University of Maryland