


Next: Generative Process Planning
Up: Related Software Support
Previous: Functionality Representation
In order to perform manufacturability analysis, a product design must
be interpreted in terms of manufacturing features. Automated feature
recognition has become the preferred technique for producing such
feature-based representations, having been successfully employed for a
variety of applications including process planning and part code
generation for group technology. These feature technologies are rely
heavily on the geometric and topological manipulation capabilities of
solid modeling systems and deal predominantly with form or machining
features.
Kyprianou [110] presented the first effort to use a
grammatical approach to parse solid models of parts for group coding.
Kramer [111] has presented a grammar-based method for
extracting non-intersecting features for a class of
2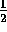 -dimensional parts. Methods based on graph-grammars
have been used to both recognize features [112,113] and
translate between differing feature
representations [114]. Peters [115]
analyzes the combinatorial complexity of graph and grammatical
approaches to feature recognition and presents heuristics to reduce
these costs. In another effort to to address combinatorial problems
and handle realistic industrial designs, Gadh and
Prinz [116] describe techniques for abstracting an
approximation of the geometric and topological information in a solid
model and finding features in the approximation. More recently, Regli
et al [117] have outlined methods to
utilize multiple distributed processors. Their initial results show
that multi-processor techniques can be effectively employed to
significantly expand the class of mechanical designs that are feasible
and produce large improvements in system response times.
-dimensional parts. Methods based on graph-grammars
have been used to both recognize features [112,113] and
translate between differing feature
representations [114]. Peters [115]
analyzes the combinatorial complexity of graph and grammatical
approaches to feature recognition and presents heuristics to reduce
these costs. In another effort to to address combinatorial problems
and handle realistic industrial designs, Gadh and
Prinz [116] describe techniques for abstracting an
approximation of the geometric and topological information in a solid
model and finding features in the approximation. More recently, Regli
et al [117] have outlined methods to
utilize multiple distributed processors. Their initial results show
that multi-processor techniques can be effectively employed to
significantly expand the class of mechanical designs that are feasible
and produce large improvements in system response times.
Woo [118], in an early effort on feature extraction,
proposed a method for finding general depression and protrusion
features on a part through decomposing the convex hull of the solid
model. The approach had several limitations, including the existence
of pathological geometric cases in which the procedure would not
converge. The non-convergence of Woo's approach has been solved in
recent work by Kim [119,120,121], whose
system produces a decomposition of the convex hull of a part as
general form features. Extension of this method from polyhedra to the
more general surfaces required for realistic parts is currently under
investigation [122].
Other volume decomposition approaches include the recent work by
Sakurai [123]. Exhaustively, each
combination of cells is then matched against user-defined feature
templates. While the method is capable of generating all alternative
feature interpretations composed of the primitive cells, it does so at
a large combinatorial cost.
The seminal work of Henderson [124] employed rule-based
systems on the feature recognition problem and has served as a
foundation for more recent AI-based approaches. Henderson has also
made extensive use of graph-based methodologies, first
in [125] where graph-based algorithms
are used to find protrusion and depression features. In Chuang and
Henderson [126] use graph-based pattern matching to
find feature patterns from part geometry and topology. Chuang and
Henderson [127] were the first to explicitly
address both computational complexity and decidability when defining
the feature recognition problem. Their paper formalized the problem
of recognition of features (including compound features) through
parsing a graph-based representation of a part using a web grammar.
Most recently, Gavankar and Henderson [128] adapted
neural networks to recognize features from polyhedral objects. Also
in this area, Peters [129] describes techniques for
training neural networks to recognize feature classes that can be
customized by the end user. In a recent paper, Henderson et
al. [130] surveys a variety of feature recognition
methodologies.
Other graph-based methodologies include the work of De
Floriani [131], who employed graph-based algorithms for
finding bi-connected and tri-connected components to partition a
polyhedral part into several varieties of protrusion and depression
features. Joshi's [132] approach used subgraph isomorphism
algorithms to match feature patterns to patterns in the topology of
polyhedral parts. Sakurai [133] developed a
graph-based system capable of handling limited types of user-defined
features, providing for a degree of application-specific
customizability. Corney and
Clark [134,135] have had success
extending the capabilities of graph-based algorithms to more general
2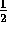 -dimensional parts.
-dimensional parts.
The work of Dong and Wozny [136,137,138]
included formalization of a feature description language and was the
first to employ a frame-based reasoning system to extract machining
features for computer-aided process planning. Their approach included
the ability to construct volumetric features from surface features and
perform an analysis of tool accessibility.
Karinthi and Nau [139] presented the first
systematic work on the generation of alternative interpretations of
the same object as different collections of volumetric features. They
present an algebra for computing alternate interpretations of parts
resulting from algebraic operations on the features.
The ability to recognize interacting features has been a goal of a
number of numerous research efforts, among
them [116,132,136]. The approach of
Marefat [140,141] built on the
representation scheme of Joshi [132] and used a combination
of expert system and hypothesis testing techniques to extract surface
features from polyhedral objects and handle a variety of their
geometric interactions. Marefat argues that his approach is complete
over a class of polyhedral features, i.e., that it generates all
features in his class that can be found from the geometry a part.
Another recent approach [142] addresses completeness
over a limited domain of iso-oriented polygonal parts. Regli et
al [143,144] present a methodology for specifying
the feature recognition problem and proving it is complete over a
well-defined class of parts. Their features are based on a class of
machining features that describe operations on three-axis machining
centers and encompass a realistic class of parts bounded by analytic
surfaces.
The most comprehensive approach to date for recognizing features and
handling their interactions has been the OOFF system (Object-Oriented
Feature Finder) of Vandenbrande [145]. Vandenbrande's
work, using a knowledge-based approach like that of Dong and Wozny,
provides a framework for recognizing machining features and building
process plans via artificial intelligence techniques in combination
with queries to a solid modeler.
Work of Laakko and Mäntylä [146] couples
feature-based design and feature recognition to provide for
incremental feature recognition. This type of approach identifies
changes in the geometric model as new or modified features while
preserving the existing feature information. They also provide for
some form of customizability with use of a feature-definition language
to add new features into the system.
Other related work includes feature recognition from 2D engineering
drawings [147], feature recognition for sheet-metal
components [148], and feature modeling by
incremental recognition [146]. Many aspects of
the feature recognition problem are still open and active areas of
research. Among these are: recognizing and representing interacting
features [145], incremental recognition of
features [149], modeling alternative feature
interpretations [140,143], reasoning about the
manufacturability of features [25,150], and
incorporation of user-customizable feature classes.



Next: Generative Process Planning
Up: Related Software Support
Previous: Functionality Representation
Generated by latex2html-95.1
Fri Apr 14 13:59:16 EDT 1995
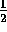 -dimensional parts. Methods based on graph-grammars
have been used to both recognize features [112,113] and
translate between differing feature
representations [114]. Peters [115]
analyzes the combinatorial complexity of graph and grammatical
approaches to feature recognition and presents heuristics to reduce
these costs. In another effort to to address combinatorial problems
and handle realistic industrial designs, Gadh and
Prinz [116] describe techniques for abstracting an
approximation of the geometric and topological information in a solid
model and finding features in the approximation. More recently, Regli
et al [117] have outlined methods to
utilize multiple distributed processors. Their initial results show
that multi-processor techniques can be effectively employed to
significantly expand the class of mechanical designs that are feasible
and produce large improvements in system response times.
-dimensional parts. Methods based on graph-grammars
have been used to both recognize features [112,113] and
translate between differing feature
representations [114]. Peters [115]
analyzes the combinatorial complexity of graph and grammatical
approaches to feature recognition and presents heuristics to reduce
these costs. In another effort to to address combinatorial problems
and handle realistic industrial designs, Gadh and
Prinz [116] describe techniques for abstracting an
approximation of the geometric and topological information in a solid
model and finding features in the approximation. More recently, Regli
et al [117] have outlined methods to
utilize multiple distributed processors. Their initial results show
that multi-processor techniques can be effectively employed to
significantly expand the class of mechanical designs that are feasible
and produce large improvements in system response times.
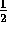 -dimensional parts.
-dimensional parts.