News Story
Galloway, Justh, Krishnaprasad publish chasing and flocking research in Proceedings of the Royal Society A

Flocks of European starlings exhibiting collective behavior. Photo credit: Andrea Cavagna.
Scientists are asking these kinds of questions as they seek to unlock the mysteries of nature's collective behavior strategies, biological rules that are increasingly important to engineers creating networked systems of robots.
New research by a team of University of Maryland alumni and faculty published in the current issue of the Proceedings of the Royal Society A explores how strategies, feedback laws and attentional graph structure influence the space-time evolution of collective dynamics. The researchers developed nonlinear dynamical models and a family of equations that can help analyze the collective behavior that emerges from the actions of individuals. These action strategies are leading to biologically plausible modes of pairwise interaction.
"Symmetry and reduction in collectives: cyclic pursuit strategies" was written by two University of Maryland alumni, Commander Kevin Galloway (EE Ph.D. 2011), an assistant professor in electrical and computer engineering at the U.S. Naval Academy; and Eric Justh (EE Ph.D. 1998), an electronics engineer at the Naval Research Laboratory; and Professor P. S. Krishnaprasad (ECE/ISR).
Using interaction symmetries and reduction of the dynamics to the shape-space of the collective, the authors derived solutions predicting spatio-temporal patterns. They also elucidated the influence of control parameters on collective behavior.
Behind the team's mathematical formulations is curiosity about both how nature works and the way collective behavior can be translated to engineered networks of robots.
Towards a better understanding of nature
The research also suggests interesting hypotheses concerning possible underlying mechanisms for the impressive displays of collective motion observed in nature, such as the circular schooling behaviors which some species of fish exhibit for protection against predators.
"I was originally drawn to this research by the fascinating—and sometimes surprising—way in which relatively simple local interactions between individual agents in a collective give rise to complex and beautiful maneuvers for the larger group," Galloway says. "One might expect that coordinated circling patterns or spiral maneuvers that maintain the shape of a formation must require some type of external orchestration or group leadership, and yet here we find these very behaviors arising from pursuit encounters played out at the level of the individual agents."
"The special solutions to these equations yield behaviors consistent with biological settings such as flocking birds, foraging dolphins and ant mills," says Krishnaprasad.
While this research focused on a uniform constant bearing (CB) strategy used by all agents in a collective, it is also possible to consider heterogeneous pursuit strategies in both natural and artificial settings. Different kinds of individual behavior may arise from strategy preferences of individuals based on the context and their sensory capabilities. The methods used in this paper also lend themselves to analyzing these richer settings.
One problem being pursued by Krishnaprasad and his students is the analysis of three-dimensional position data from observations of large flocks of European starlings, numbering in the hundreds and displaying striking flight behavior. This data was provided by Dr. Andrea Cavagna, a collaborator from Italy.
"We are analyzing this data using a variety of techniques, including some from optimal control theory," Krishnaprasad says. "Here the relevant attention graphs are dynamic and pose challenges for the modeler. Observations of such natural flocks pose inverse problems—reconstructing smooth trajectories from sampled data; determining statistical characteristics of interactions among members of a flock; and inferring underlying sensori-motor feedback laws, taking into account delays between perception and action, and stochasticity."
Implications for robotics
These insights from the study of nature can be used to devise algorithms for collective behavior in robotics. Problems of implementation of robot control algorithms give impetus to the creation of software environments for motion programming, says Krishnaprasad. "For a number of years, I have been working with students to demonstrate such tools on mobile robots in our Intelligent Servosystems Laboratory. Recently we have inaugurated a testbed that uses motion capture technology to explore ideas and algorithms in cooperative autonomous robots."
The research suggests engineering applications for networked robots such as unmanned aerial or ground vehicles working together for a collective purpose. "We are providing a framework for designing control strategies to generate coordinated maneuvers without requiring unrealistic communication and sensing capabilities," Galloway says. In addition, "there is also potential for application of related mathematical methods to biped robotics, where 'agents' in a collective (e.g. the joints of a biped robot, connected by mechanical linkages) are required to move in a coordinated manner to achieve a macro-scale objective such as walking over rough ground."

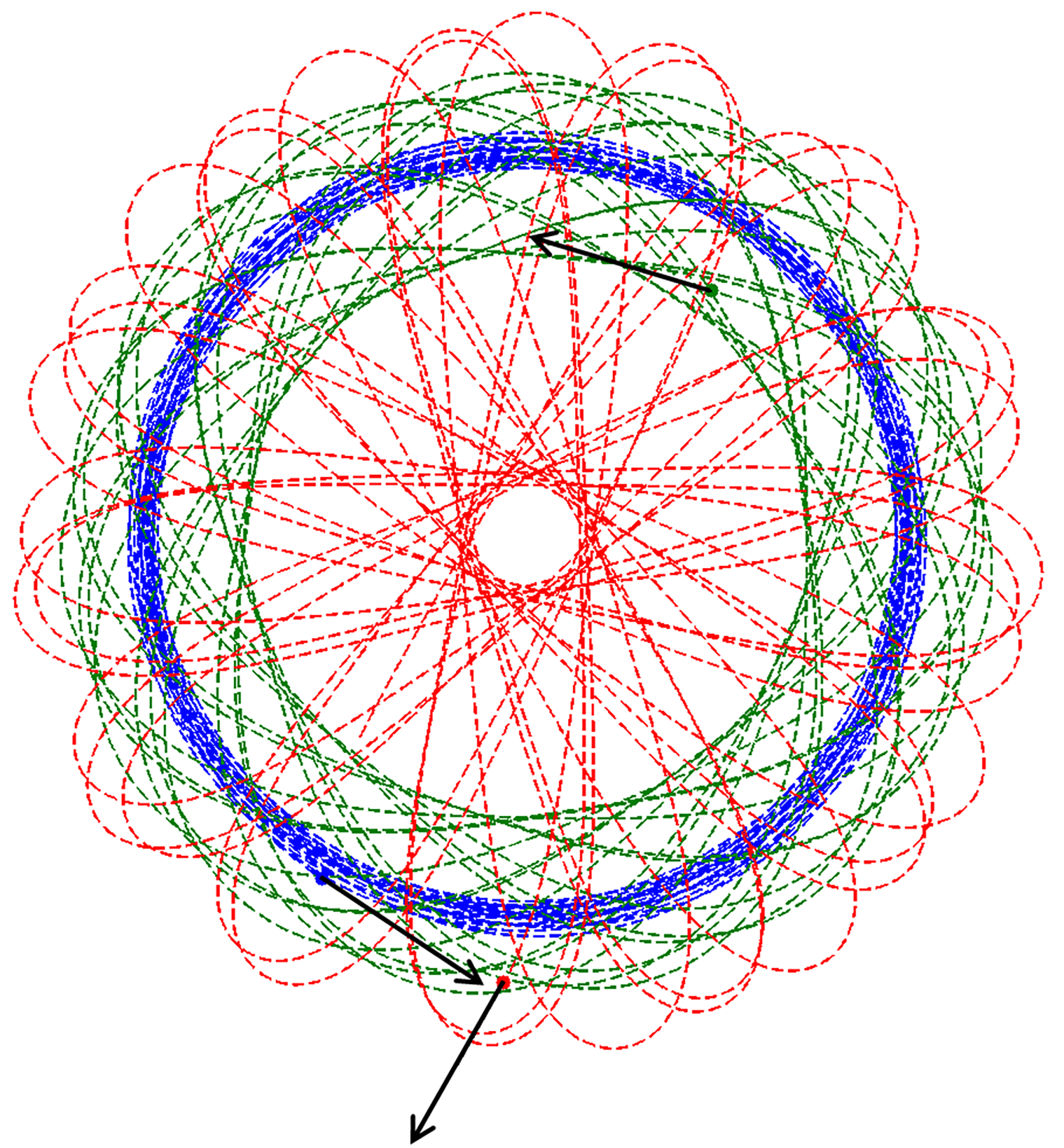
Screen shot of steady motions of a collective of particles subject to an interaction strategy known as constant bearing (CB) pursuit, under four different conditions on the control parameters. These lead to observed special motions identifiable as pure shape equilibria (spiraling and focal expansion) in the top half, and shape equilibria (circling and rectilinear motion) in the bottom half of the figure. The methods of this paper lead to predicting conditions that produce such special motions, from a combination of interaction strategy, graph structure of interactions (here a pure cycle graph) and symmetry. Using the special motions as building blocks, it is possible to analyze complex collective behavior observed in nature (flocking, foraging, etc.), and also synthesize such behavior in control software for groups of robots. Photo credit: Intelligent Servosystems Laboratory, University of Maryland
- - - - - - - - - - - - -
View the paper online (subscription required for full text)
Additional resources: videos
Watch four patterns emerge from convergence to steady collective motions. These animations display convergence of collective motion to certain steady state solutions. "Spiral" and "Focal expansion" correspond to pure shape preserving motions, while the size of collective expands; "Rectilinear" and "Circling in CB pursuit" correspond to size and shape preserving motions.
| Spiral | Focal expansion | Rectilinear | Circling in CB pursuit |
Watch a video of European starlings exhibiting collective behavior, courtesy of Andrea Cavagna.
Additional resources: photos
High-resolution photo of the four patterns of collective motion Credit: Intelligent Servosystems Laboratory, University of Maryland
High-resolution photo of European starlings flocking Credit: Andrea Cavagna |
Additional resources: PPT and photos
Photos of naturally occurring collective behavior and a short PowerPoint presentation with videos and explanations of the algorithms in this research are available here.
Dr. Krishnaprasad's research
Links to papers on this subject written by Dr. Krishnaprasad and his colleagues are accessible from this PDF file.
To learn more about Dr. Krishnaprasad's work, see videos and slides of his lectures, and access his papers, visit his personal website.
- - - - - - - - - - - - -
Published August 17, 2013