News Story
Small collectives and nonlinear dynamics
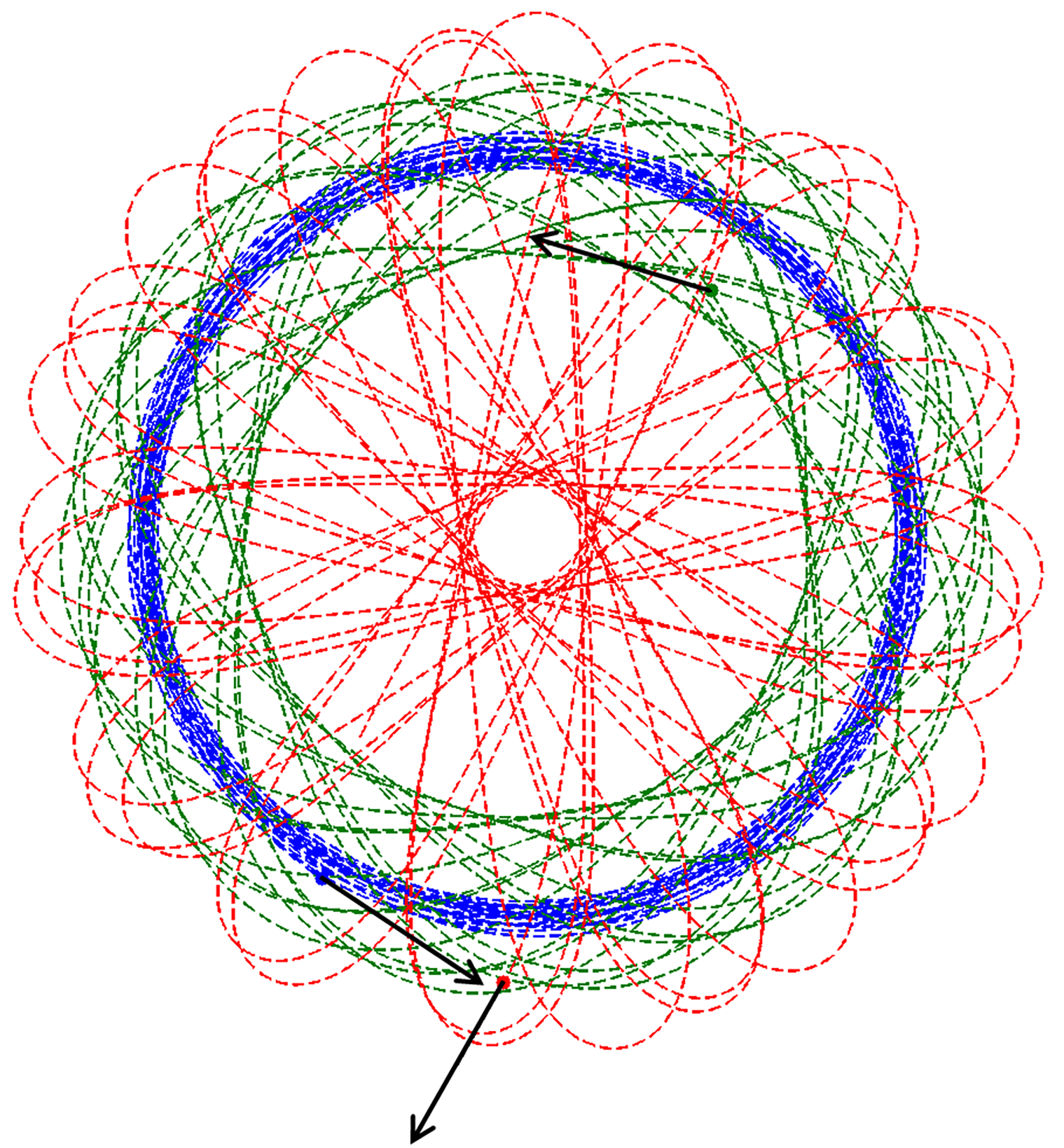
Planar precession of three particles (Figure 7a of the paper; screenshot from animation created by K. S. Galloway; copyright Royal Society)
Imagine a hiker lost in an overgrown forest or hard-to-access mountainous region, seeking and failing to get back to the trail and desperately needing to be rescued. Or consider the possibility of a lone sailor adrift in the open ocean and low on supplies, hoping that distress signals from the boat would draw the attention of Coast Guard vessels. In such situations enormous effort is often expended to save lives, at great cost and risk to the first responders.
Would a small team of cooperating, unmanned autonomous aerial vehicles provide an effective alternative to current solutions based on personnel- and equipment-intensive operations? The answer depends on our ability to design and implement intelligent behaviors in such collectives, using feedback control laws that can realize patterns of persistent search and tracking, and actions based on detecting targets of interest.
While many technological issues—such as, on-board power, sensing and computational resources, and platform design—merit consideration, the mathematical challenges of creating and sustaining mobility patterns are no less worthy of attention. The authors of a new paper, “Symmetry and reduction in collectives: low dimensional cyclic pursuit,” published October 26 in the Proceedings of the Royal Society A, investigate the types and stability of motion patterns in controlled small collectives. The journal website includes supplementary material in the form of animations of small collectives.
The paper was written by U.S. Naval Academy Assistant Professor Kevin Galloway (ECE Ph.D. 2011), Naval Research Laboratory Electronics Engineer Eric Justh (ECE Ph.D. 1998), and University of Maryland Professor P. S. Krishnaprasad (Electrical and Computer Engineering/Institute for Systems Research). They use an abstraction of agents in a collective as self-steering particles interacting according to a strategy known as constant bearing cyclic pursuit, to develop an understanding of spatial motion patterns.
In the case of collectives with two or three agents, they predict the presence of periodic orbits in phase space and precession in physical space. Key elements of the work include exploitation of nonlinear feedback laws to execute the strategy, and use of rigid motion group symmetry and reduction to shape space, as (detailed) in their earlier collaboration, also published in the Proceedings of the Royal Society A. The presence of periodic orbits in the case of small collectives supports the possibility of using associated control laws to guide a team of vehicles to achieve coverage and persistent surveillance for purposes such as search and rescue. Recent developments in the work of Galloway, Biswadip Dey and Kenneth Miltenberger Jr. show that these ideas can be taken further to practical implementations (missions in a test-bed).
The mathematics underlying the current paper has modern control-theoretic aspects as well as classical roots. In recognizing the presence of time-reversal symmetry in the problem of small collectives, the authors use a theorem of G. D. Birkhoff from his studies in 1915, on three body problems of Newtonian particles bound by gravitation. It is rewarding that one can build intellectual bridges between problems arising from widely separated concerns.
There are other threads to explore, such as how small collectives are embedded as network motifs in larger multi-agent systems, and whether this would lead to insights into the behavior of complex interacting systems in nature and in the engineered world.
Published November 9, 2016